Archives de catégorie : Sciences – Techniques

Le problème des trois corps

Par Ben Hunt – Le 21 décembre 2017 – Source Epsilon Theory – Source : Le Saker Francophone
Même si je n’aime pas les poulets de notre ferme, j’adore mes abeilles. Est-ce qu’elles piquent ? Bien sûr qu’elles piquent. L’essaim est un animal sauvage. Mais après quelques années douloureuses, je ne suis plus aussi maladroit avec mes ruches, et une matinée passée en synchronisation avec cet animal incroyable n’est jamais une mauvaise matinée. Non seulement les abeilles n’ont pas besoin d’un entretien particulier, non seulement elles paient un loyer formidable, mais elles font preuve de génie et d’optimisme – il n’y a pas d’autre mot – qui me font me sentir plus créatif et vivant.

Les hivers du Connecticut sont rudes. Je fais ce que je peux pour soutenir les abeilles, c’est-à-dire construire un brise-vent avec des balles de paille, m’assurer que la ruche reste suffisamment ventilée pour empêcher la condensation de vapeur d’eau et empêcher les souris de s’y installer. Cela et éviter les péchés originels comme le mauvais placement de la ruche ou la perception d’un loyer trop élevé. Mais en fin de compte, c’est une bataille entre l’animal et Mère Nature. C’est à elles de survivre. Ou pas.

Les abeilles n’hibernent pas (les bourdons le font, mais pas les colonies d’abeilles domestiques), et elles ne peuvent pas voler vers le sud pendant l’hiver. Pour survivre à un hiver nordique, les abeilles modifient la composition de l’essaim en réduisant la population globale, en calfeutrant la ruche, en se débarrassant des mâles qui sont un poids mort (c’est-à-dire de TOUS les mâles) et en pondant juste assez d’œufs pour préserver une population minimale pouvant survivre pendant l’hiver et au printemps. Elles se regroupent au centre de la ruche, gardant la reine au centre, faisant vibrer leurs ailes pour créer de l’énergie cinétique, envoyant à l’occasion des escouades suicides pour récupérer du miel dans les rayons extérieurs. Elles réduisent leur métabolisme en créant un nuage de dioxyde de carbone dans la ruche. Oui, un nuage de dioxyde de carbone.

Toute cette préparation prend du temps. Pour survivre à l’hiver, l’essaim commence à changer de comportement – des modèles de couvain à la collecte du pollen en passant par la création de peignes – non pas quand le temps commence à refroidir, mais au milieu de l’été quand les journées les plus chaudes d’août sont encore là. Et pas juste à une date au hasard, mais un jour complètement prévisible.

En 2018, mes abeilles commenceront à se préparer pour l’hiver le vendredi 22 juin.

Pourquoi ? Parce que les abeilles peuvent mesurer l’angle des rayons du soleil. Elles peuvent s’en souvenir d’un jour à l’autre. Quand le soleil de midi d’aujourd’hui sera un peu plus bas dans le ciel que le soleil de midi d’hier, une abeille le saura. Et toute la colonie commencera à changer.

Les abeilles reconnaissent le solstice d’été avec autant de précision que n’importe quelle civilisation humaine.

Tu vois ? Du génie. Mais cela ne fait que commencer.

Lorsque les abeilles agissent en fonction de leur connaissance du solstice d’été, elles échangent un produit dérivé. Et elles gèrent de manière experte le risque de base de ce commerce.

Hein ? Temps mort, Ben. Qu’est-ce que tu racontes ?

Un produit dérivé, au sens le plus large du terme, est quelque chose qui est lié à quelque chose d’autre qui vous tient à cœur (le « sous-jacent »), mais pour quelque raison que ce soit, vous choisissez d’interagir avec le dérivé de ce quelque chose plutôt que le sous-jacent de ce quelque chose. Pour les humains, le cours de l’action de la société XYZ peut vous préoccuper, ce qui implique le sous-jacent, mais si vous pensez qu’il va arriver quelque chose d’important à la société dans trois mois, alors vous interagissez avec un dérivé sur l’action, dans ce cas un contrat d’option à trois mois. Pour les abeilles, ce qui les intéresse vraiment, c’est le froid qu’il fait, donc, de leur point de vue, la température est le sous-jacent et les angles d’ensoleillement en sont le dérivé qu’elles analysent et avec lequel elles interagissent. En vérité, bien sûr, c’est l’inclinaison de l’axe de la Terre et les angles d’ensoleillement qui en résultent qui causent les variations saisonnières et les changements de température, alors un lecteur un peu pointilleux pourrait dire avec exactitude que c’est la température qui est le dérivé ici, mais je crois que nous sommes tous assez ouverts pour avoir une vue du monde du point de vue des abeilles pendant toute cette note.

Pourquoi les abeilles adoptent-elles leurs signaux comportementaux en fonction de l’angle d’ensoleillement plutôt que des changements de température directs ? Parce que l’algorithme de prévision de la saisonnalité – SI (angle d’incidence maximal de la lumière du soleil aujourd’hui < angle d’incidence maximal de la lumière du soleil hier), ALORS (se préparer pour l’hiver) – est bien plus simple, plus prédictif, plus opportun et moins volatile que toute analyse chronologique de la température, ou au moins toute analyse chronologique des températures disponible aux abeilles et aux humains avant les satellites météorologiques. Le génie (et le défaut fatal) des abeilles et des humains est leur capacité à créer des systèmes sociaux complexes sur la base d’algorithmes simples comme celui-ci. Les systèmes informatiques modernes du type Big Data ont un type de génie très différent.

Gardez cette pensée en tête.

Mais d’abord, assurons-nous de bien comprendre ce que signifie le risque de base et pourquoi c’est la chose la plus importante à comprendre lorsqu’il s’agit de dérivés. La « base » est la relation entre le dérivé et le sous-jacent, et le risque de base est donc de savoir à quel point les choses pourraient se détériorer si la relation entre le dérivé et le sous-jacent n’est pas aussi étroite que vous le pensiez. Pour les abeilles, le risque de base prend la forme d’un temps froid qui survient plus tôt ou plus tard par rapport à la normale. Rétrécir la colonie comme une horloge basée sur le solstice d’été fonctionne très bien si le premier gros gel survient en novembre, pas très bien s’il y a une grosse neige à la mi-octobre.

La clé de la gestion du risque de base est de garder vos antennes de risque (littéralement les antennes quand il s’agit d’abeilles) concentrées sur la façon dont la chose dérivée est liée avec la chose sous-jacente. Vous devez surveiller la corrélation. Ainsi, pour gérer leur risque de base, les abeilles sont également sensibles à la température (le sous-jacent) et à tous les autres facteurs dérivés liés aux changements de température, comme la floraison des fleurs ou les vents dominants. Rien ne l’emportera totalement sur la survenue du solstice d’été (même les abeilles tropicales font quelques petits ajustements de colonies en fonction de la saisonnalité), mais les abeilles sont des investisseurs adaptatifs, capables d’accélérer leur préparation hivernale si le temps froid arrive tôt ou de le retarder si le temps froid arrive tard. Une gestion efficace du risque de base est un exercice d’équilibre entre le maintien du commerce original et l’adaptation de votre comportement aux corrélations changeantes (vous ne voulez pas confondre un été indien avec le printemps !), mais c’est la beauté de l’évolution – des milliards de colonies d’abeilles ont vécu, sont mortes et se sont reproduites au fil des ans pour sélectionner la combinaison des algorithmes du système nerveux qui permet aux abeilles de se multiplier dans une vaste gamme d’écosystèmes et une multitude de variations météorologiques.

Mais ce n’est qu’un exemple. Les abeilles ne peuvent pas vivre dans une aussi grande variété d’écosystèmes et de variations météorologiques que, disons, les fourmis. Je doute qu’il y ait une colonie d’abeilles sur Terre qui puisse survivre six mois à -50 degrés. Si vous êtes une colonie d’abeilles et que vous avez déménagé aussi loin au nord que possible augmentant l’ampleur de votre risque de base, peu importe à quel point vous êtes futé dans vos calculs de déclinaison solaire… vous n’allez pas y arriver. Peut-être aurez-vous de la chance pendant quelques années, mais s’il est possible que vous ayez quatre ou cinq mois de temps vraiment très froid, alors tôt ou tard, le risque de base sévère vous rattrapera. C’est un risque de base contre lequel vous ne pouvez pas vous assurer, contre lequel vous ne pouvez pas vous prémunir avec une préparation ou des précautions supplémentaires. C’est un risque de base ingérable. Pour la plus grande partie de l’Amérique du Nord, cependant, même assez loin au Canada, le temps froid est un risque de base gérable, surtout si vous avez un apiculteur capable de vous prêter main-forte. Parfois, les abeilles auront un mauvais lancer des dés météorologiques et vous perdrez une ruche face au risque de base, mais cela ne menace pas l’espèce.

Le risque pour les espèces entre en jeu lorsqu’un événement climatique majeur dure longtemps en termes de durée de vie d’une colonie, mais pas longtemps en termes d’évolution, de mutation génétique et de sélection naturelle. Et si le printemps ne suivait plus l’hiver ? Et s’il neigeait en août et que les fleurs fleurissaient en janvier ? Et si l’hiver disparaissait pendant une décennie ? Et si ça durait si longtemps ? Et si votre risque météorologique était inconnaissable, comme dans Game of Thrones ? Même un bref hiver à Westeros de quelques années tuerait toutes les colonies d’abeilles du continent, c’est pourquoi je ne pense pas avoir jamais vu une ruche d’abeilles dans Game of Thrones. [Je viens d’être informé par le Grand Mestre Guinn que l’une des maisons vassales de Baratheon dans le Reach est la Maison « Beesbury », avec un siège familial à Honeyholt et une devise familiale « Attention à mon dard. » Soupir. Tu vois ce que je dois supporter ? Ok, nous allons stipuler que les latitudes dorniennes sont sûres. Mais le Nord n’est pas un endroit pour les abeilles quand l’hiver vient !].

Il s’agit d’une incertitude de base, où vous n’êtes même pas certain qu’il existe une quelconque base, par opposition à un simple risque de base. L’incertitude de base est un risque de base inconnaissable, qui est beaucoup plus dommageable pour le développement des espèces que l’apparition occasionnelle d’un sévère risque de base.

Entre parenthèses : la compréhension de la distinction entre risque et incertitude est cruciale dans tous les aspects de la vie. Une décision risquée, c’est quand on a une bonne idée des chances et des gains. Elle se prête à l’analyse statistique et à l’économétrie, surtout si c’est une décision que vous aurez l’occasion de prendre plusieurs fois. Une décision incertaine, c’est quand vous n’avez pas une bonne idée des probabilités et des gains. Ici, l’analyse statistique peut très bien vous tuer, surtout si vous n’allez pas avoir beaucoup de fissures dans le jeu, ou si vous ne savez pas combien de fois vous aurez à faire un choix. Vous avez besoin de la théorie des jeux pour comprendre les décisions prises dans l’incertitude.

L’incertitude de base est le problème central auquel tous les investisseurs sont confrontés aujourd’hui.

Ce n’est pas seulement le fait que nous endurons de grands risques de base ici sur ce marché faussé, ingérables pour beaucoup. Ce n’est pas seulement que tous nos vieux poteaux indicateurs et amarres pour naviguer sur les marchés ne fonctionnent pas très bien. Il n’est pas seulement difficile d’identifier des modèles prédictifs ou dérivés dans les marchés actuels. Il y a une chance non négligeable que les changements structurels dans nos mondes sociaux de la politique et des marchés aient rendu impossible l’identification de modèles prédictifs/dérivés. C’est l’incertitude de base, et c’est aussi problématique pour les humains qui font face à des marchés qui n’ont pas plus de sens que régimes climatiques pour les abeilles.

C’est de la folie, Ben. Que voulez-vous dire par là qu’il pourrait être impossible d’identifier des modèles prédictifs/dérivés ? Comment ça, cette base n’existe peut-être pas du tout ? Bien sûr, il y a un modèle pour les marchés et tout le reste. Bien sûr, le printemps suit l’hiver.

Non, non. C’est le problème des trois corps.

Ou plutôt, le problème des trois corps est un exemple célèbre d’un système qui n’a pas de modèle dérivé avec une quelconque puissance prédictive, aucun algorithme applicable qu’un humain (ou une abeille) pourrait découvrir pour s’adapter avec succès et transformer une incertitude de base en risque de base. Dans le jargon, il n’y a pas de « solution générale sous forme fermée » au problème des trois corps. (C’est aussi le titre du meilleur livre de science-fiction que j’ai lu au cours des 20 dernières années, de Cixin Liu. Vraiment un chef-d’œuvre. La vie et le changement de perspective, en fait, à la fois dans sa représentation de la Chine et dans sa représentation de la théorie des jeux de la civilisation.)

Quel est le « problème » ? Imaginez trois objets massifs dans l’espace… des étoiles, des planètes, quelque chose comme ça. Ils sont dans le même système, ce qui signifie qu’ils ne peuvent pas échapper entièrement à l’attraction gravitationnelle les uns des autres. Vous connaissez la position, la masse, la vitesse et la direction de déplacement de chacun des objets. Vous connaissez le fonctionnement de la gravité, donc vous savez exactement comment chaque objet agit sur les deux autres objets. Maintenant, prédisez pour moi, à l’aide d’une formule, où les objets se trouveront à un moment donné dans l’avenir.

Réponse : vous ne pouvez pas. En 1887, Henri Poincaré prouve que le mouvement des trois objets, à l’exception de quelques cas particuliers de départ, est non répétitif. Il s’agit d’un système chaotique, ce qui signifie que le modèle historique des positions des objets a un pouvoir prédictif nul pour ce qui est de déterminer où ces objets se trouveront à l’avenir. Il n’y a pas d’algorithme qu’un humain puisse découvrir pour résoudre ce problème. Cela n’existe pas.

Pour visualiser le problème des trois corps, voici une simulation des orbites d’objets verts, bleus et rouges avec des conditions de départ aléatoires, chacun exerçant une attraction gravitationnelle sur les autres. Ce que Poincaré a prouvé, c’est qu’il n’y a pas de formule où vous pouvez brancher l’information initiale et obtenir la bonne réponse pour savoir où l’un des objets sera à tout moment dans le futur. Aucun humain ne peut prédire l’avenir de ce système.

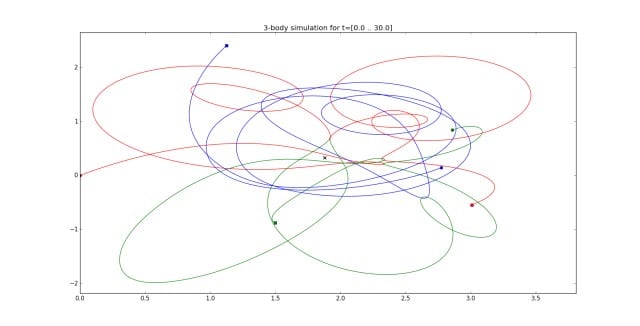
Mais un ordinateur peut le faire. Non pas en utilisant un algorithme, qui est la façon dont les cerveaux biologiques – humains et abeilles – ont évolué pour donner un sens au monde, mais par des calculs de force brute. Rappelez-vous, vous savez tout au sujet de ces trois objets… aucune loi de la physique ici n’est un mystère. Si vous pouvez faire le calcul assez rapidement, vous pouvez calculer où les trois objets seront dans une seconde à partir de maintenant. Et dans une autre seconde. Et ainsi de suite et ainsi de suite. Avec une puissance de traitement suffisante (et cela peut nécessiter beaucoup de puissance de traitement), vous pouvez calculer où se trouveront les trois objets dans 100 ans, même s’il est impossible de résoudre ce résultat avec des équations.

C’est un concept difficile à comprendre, cette différence entre calculer l’avenir et prédire l’avenir, mais elle changera votre façon de voir le monde. Et votre place là-dedans.

Voici une observation sur laquelle je ne saurais que trop insister, pourtant je vais essayer :

CE N’EST PAS AINSI QUE NOUS UTILISONS LES ORDINATEURS DANS NOS STRATÉGIES D’INVESTISSEMENT AUJOURD’HUI

La façon dont les ordinateurs peuvent calculer une réponse au problème des trois corps est simple – ils peuvent être programmés avec les règles de la physique pour savoir comment un objet influence un autre objet, afin de pouvoir simuler où chaque objet ira ensuite. Il n’y a aucun examen de l’endroit où les objets ont été dans le passé. Il s’agit d’une vision entièrement tournée vers l’avenir.

La façon dont les ordinateurs ne peuvent PAS calculer une réponse au problème des trois corps est d’examiner les données historiques de l’endroit où les objets ont été. Dans un système chaotique, peu importe la difficulté, la rapidité ou la profondeur de l’examen des données historiques. Il n’y a AUCUN modèle prédictif, AUCUN algorithme secret caché dans les données. Et pourtant, c’est exactement ce que font tous nos ordinateurs… examiner les données historiques pour chercher des modèles qui nous donneront l’algorithme magique pour prédire ce qui va suivre ! La seule chose que le passé vous donne dans un système chaotique est l’inertie, qui peut ressembler à un modèle ou à un algorithme pendant un certain temps, selon la façon dont tous les objets sont alignés. Mais c’est un mirage. Cela ne dure pas. Examiner le passé d’un système chaotique peut vous donner beaucoup de petites réponses, comme les étincelles d’un feu de joie, qui ne durent que quelques secondes. Et certainement, si vous êtes efficace avec votre effort de capture d’étincelles d’identification de l’inertie, vous pouvez faire de l’argent en utilisant les ordinateurs de cette façon. Mais cet examen du passé par induction naïve ne vous donnera jamais La réponse. Parce que La Réponse n’existe pas dans le passé. La Réponse – qui est un autre mot pour algorithme, qui est un autre mot pour « solution générale fermée » – n’existe pas dans un système chaotique à trois corps.

Mais on peut faire une approximation de la réponse. Nous pouvons calculer l’avenir en petits blocs de calcul, même si nous ne pouvons pas prédire l’avenir d’un seul coup, mais seulement si nous pouvons programmer l’ordinateur avec la « physique » du fonctionnement de la « gravité » dans les systèmes sociaux comme les marchés. Quel est l’équivalent dans notre monde financier d’une théorie de la gravité ? Je pense que c’est une théorie des « narratives ». Pour moi, il s’agit d’un programme de recherche plus intéressant que l’identification de petites inerties ou la capture de brèves étincelles. Mais ce n’est pas là où nos ressources informatiques sont allouées, parce qu’il n’y a pas d’argent mis là dedans. Pour l’instant.

L’exploration d’une théorie des « narratives », ce que j’ai appelé la machine narrative, est de la recherche fondamentale. Comme toute recherche fondamentale, elle n’est pas immédiatement rémunératrice et elle est donc difficile à financer. Mais ce n’est pas le plus grand obstacle. Non, le plus grand obstacle à la recherche fondamentale dans le domaine de la finance informatique est que les humains ont du mal à trouver des algorithmes et ont beaucoup de mal à imaginer qu’il est même possible de poursuivre un plan de recherche non anthropomorphe (pourquoi pas pour 10$ le mot) qui ne fouille pas les données historiques pour trouver des algorithmes prédictifs à chaque tour. On ne peut pas s’en empêcher !

Et si je vous disais que les algorithmes et les dérivés sont autant au cœur de la façon dont les humains se préparent à leur avenir financier qu’ils le sont pour les abeilles qui se préparent à leur avenir saisonnier ? Et si je vous disais que les stratégies dominantes de l’investissement humain discrétionnaire sont, sans exception, les algorithmes et les dérivés ? Et si je vous disais que ces algorithmes et dérivés étaient peut-être « élaborés » depuis une configuration « bénigne » du problème des trois corps qui non seulement pourrait ne jamais se répéter, mais en fait est certain de ne jamais se répéter parce que c’est un système chaotique ?

Je vais vous donner deux exemples d’algorithmes d’investissement et de produits dérivés influents. Il y en a beaucoup d’autres.

BONNES ENTREPRISES => BONNES ACTIONS

BONS PAYS => BONS EMPRUNTS D’ÉTAT

Ce sont les principes centraux de la sélection des titres et de la sélection des obligations souveraines, respectivement. Dans les deux cas, la bonté (comme la beauté) est dans l’œil du spectateur, donc je ne dis pas qu’il y a une norme unique pour ce qui fait une « bonne » entreprise ou ce qui fait un « bon » ensemble de politiques macroéconomiques. Ce que je veux dire, c’est que tous ceux qui lisent cette note (y compris moi !) croient qu’il existe une relation directe entre la qualité d’une entreprise ou d’une économie (quelle que soit la façon dont vous définissez la qualité) et le prix futur des actions ou obligations liées à cette entreprise ou économie. Ce que je veux dire, c’est que tous ceux qui lisent cette note croient que le suivi de la qualité mesurable d’une entreprise ou d’une économie (le dérivé) selon un processus normalisé et répétable (l’algorithme) aura, avec le temps, une corrélation prédictive avec le prix futur des actions et obligations connexes (les titres sous-jacents).

Quels actions voulons-nous posséder ? Mais les actions d’entreprises de haute qualité, bien sûr… des entreprises avec de brillantes équipes de gestion, des bilans en béton armé, et des produits ou services merveilleux que tout le monde veut acheter. Il en va de même pour les obligations d’État, les devises, les grands indices boursiers, etc. Peut-être qu’il faudra un certain temps pour que cette foi en la Qualité porte ses fruits, mais nous croyons tous qu’elle portera ses fruits. C’est naturel, non ? Aussi naturel que le printemps suit l’hiver. Aussi naturel que les fleurs qui fleurissent en mai et la neige qui tombe en décembre. Peut-être que les fleurs fleuriront avec quelques semaines de retard et que la neige tombera quelques semaines plus tôt, mais ce n’est qu’un risque de base, et nous pouvons le gérer.

Mais si le printemps ne suit plus l’hiver ?

Je ne nous demande pas d’abandonner notre foi en la qualité. L’un des principaux corollaires du problème des trois corps est que nous n’avons pas à rejeter notre croyance que les objets 1 et 2 existent. Nous n’avons pas à nier notre foi que la qualité des entreprises est une chose réelle et qu’elle a une grande influence gravitationnelle sur le prix des actions. Nous n’avons pas à nier notre foi que la qualité des gouvernements est une chose réelle et qu’elle exerce une forte attraction sur le prix des obligations gouvernementales.

Ce que nous devons accepter, c’est qu’il y a un objet 3 qui s’est déplacé dans une position telle que sa gravité submerge complètement l’impact des objets 1 et 2. Cet objectif 3, bien sûr, est une politique monétaire extraordinaire, en particulier l’achat d’actifs financiers d’une valeur de 20 000 milliards de dollars par les quatre grandes banques centrales – la Fed, la BCE, la BOJ et la PBOC.

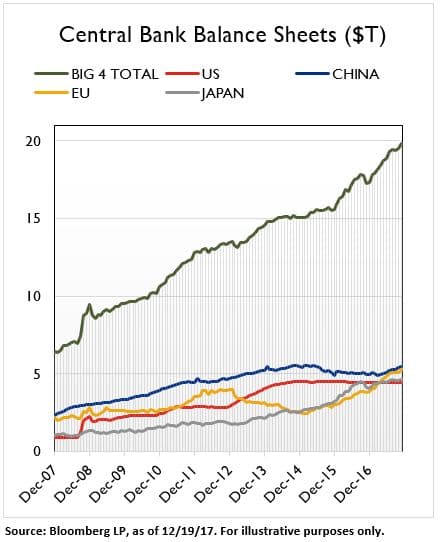
20 000 milliards de dollars, c’est beaucoup de masse. 20 000 milliards de dollars, c’est beaucoup de gravité.

Voici l’impact de toute cette gravité sur la stratégie d’investissement de la qualité des entreprises.

La ligne verte ci-dessous représente l’indice S&P 500. La ligne blanche ci-dessous est un indice de qualité sponsorisé par la Deutsche Bank. Ils examinent 1 000 sociétés mondiales à grande capitalisation et les évaluent en fonction du rendement des capitaux propres, du rendement du capital investi et de la comptabilité en terme de provisions… des approximations quantifiables des façons les plus courantes dont les investisseurs voient la qualité. Parce que l’objectif est d’isoler le facteur de qualité, l’indice est « long » en montants égaux des 20% supérieurs des entreprises mesurées et « court » sur les 20% inférieurs (donc neutre sur le marché), et a des montants égaux investis long et court dans les secteurs composants du marché (donc neutre sur le secteur). Le graphique commence le 9 mars 2009, lorsque la Fed a lancé son premier programme d’assouplissement quantitatif.

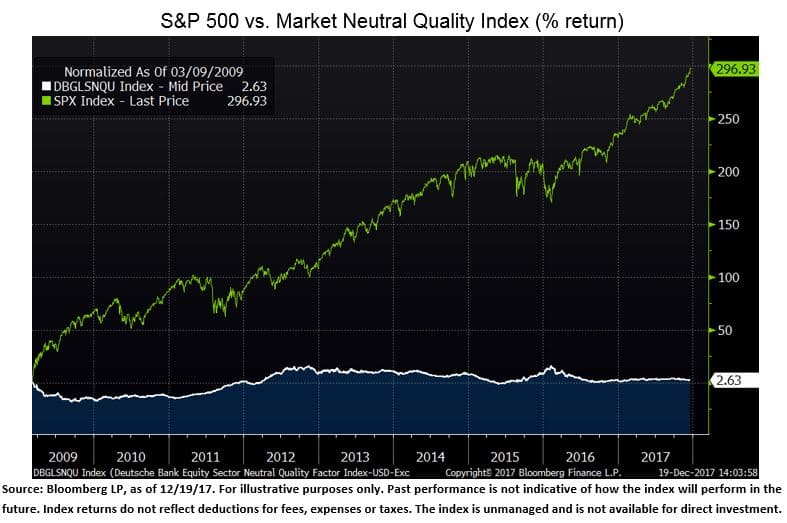
Au cours des huit dernières années et demie, la qualité s’est avérée absolument inutile en tant que dérivé de placement. Vous avez obtenu un maximal de 3% sur votre investissement, alors que le S&P 500 est en hausse de près de 300%.

Ce n’est pas une faute de frappe.

Les actions de qualité de votre portefeuille ont-elles augmenté au cours des huit dernières années et demie ? Bien sûr, mais ce n’est pas à cause de la qualité des entreprises. C’est parce que TOUTES les actions ont augmenté depuis que l’objet 3, les bilans des banques centrales, a commencé à exercer sa gravité massive sur tout Y COMPRIS les entreprises de qualité. Ce n’est pas un accident, en fait. Les banques centrales ne se soucient pas de récompenser les « bonnes » entreprises. En fait, si elles se soucient de quoi que ce soit dans cette dimension, elles se soucient d’empêcher les « mauvaises » entreprises de faire faillite.

C’est ce à quoi le monde ressemble quand le printemps ne suit pas l’hiver.

Et voici l’impact de toute cette gravité sur la stratégie d’investissement de la qualité des produits dérivés des pays.

La ligne jaune ci-dessous représente l’écart (différence) entre le rendement des obligations à 10 ans du Portugal et celui des obligations à 10 ans des États-Unis, et la ligne bleue représente l’écart entre le rendement des obligations à 10 ans de l’Italie et l’équivalent américain. En temps « normal », un pays ayant un ensemble plus faible de caractéristiques macroéconomiques (niveau élevé de dette publique, par exemple, ou peut-être faible productivité) devra offrir aux investisseurs un taux d’intérêt plus élevé pour emprunter leur argent qu’un pays ayant un ensemble plus fort de caractéristiques macroéconomiques. Ainsi, à l’été 2012, alors que le Portugal et l’Italie semblaient tous deux des pays sans succès, ils ont dû payer aux investisseurs un taux d’intérêt beaucoup plus élevé que celui des États-Unis pour attirer les investissements… environ 9 % de plus (c’est par an, remarquez-le) pour le Portugal et 4 % de plus pour l’Italie. Ce sont des écarts énormes dans le monde de la dette souveraine !

Ce graphique commence à l’été 2012, lorsque la BCE a annoncé son intention de soutenir directement le marché européen de la dette souveraine. Depuis cette annonce – même si le Portugal et l’Italie ont des ratios dette-PIB plus élevés aujourd’hui qu’en 2012 – l’écart par rapport aux taux d’intérêt américains n’a fait que diminuer. Sous l’impulsion de l’engagement de la BCE à « faire tout ce qu’il faut » et à être non seulement un acheteur de dernier recours, mais aussi un acheteur privilégié de la dette portugaise et italienne, il en coûte maintenant MOINS cher à ces pays d’emprunter de l’argent pendant 10 ans que les États-Unis.

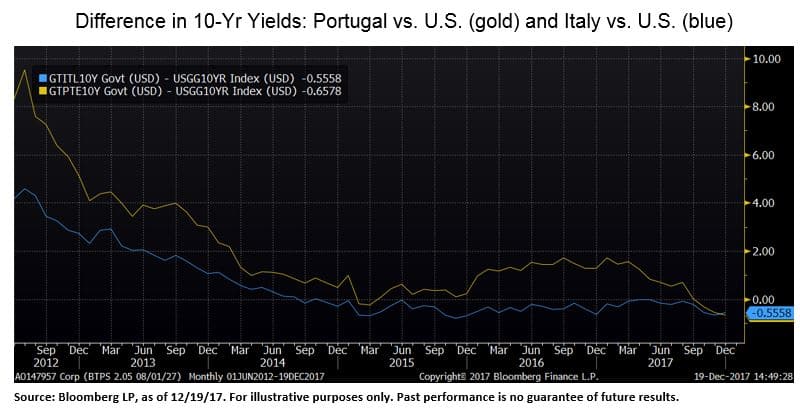
C’est de la folie. C’est compréhensible si l’on considère que le rendement des obligations allemandes à 10 ans est actuellement d’environ 30 points de base, et qu’il a été en fait négatif (ce qui signifie que vous avez dû payer le gouvernement allemand pour le privilège de leur prêter de l’argent pendant les 10 prochaines années) pendant environ six mois en 2016. Ce qui veut dire qu’au moins avec la dette italienne et portugaise, on vous paie quelque chose (un peu moins de 2% par an). C’est compréhensible si l’on considère que l’obligation suisse à 10 ans est toujours assortie d’un taux d’intérêt négatif et qu’elle l’est depuis deux ans et demi. Il y a aujourd’hui environ 10 000 milliards de dollars d’obligations souveraines à rendement négatif, ce qui est IMPOSSIBLE sous un algorithme dérivé de l’axiome [bon pays => bonne obligation]. Aucun pays n’est aussi bon ! Mais c’est tout à fait possible sous l’immense force gravitationnelle des achats massifs d’actifs par les banques centrales.

Voilà le coup de grâce. L’écart entre les obligations souveraines grecques à 10 ans et les obligations américaines à 10 ans est illustré ci-dessous. En 2012, vous avez été payé 24% de plus pour prêter de l’argent à la Grèce. Par an ! Aujourd’hui, vous êtes payé moins de 2% de plus pour prêter de l’argent à la Grèce plutôt qu’aux États-Unis. Pendant dix ans. À la Grèce.

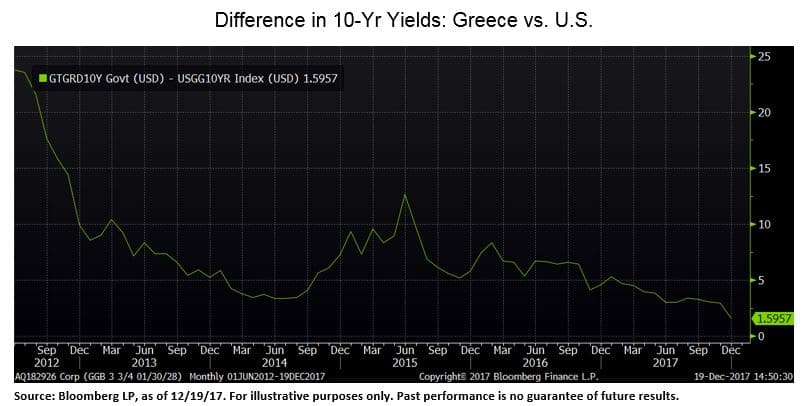
Encore une fois, je ne dis pas que la dérivée Qualité n’existe pas en tant que telle ou qu’elle n’est pas un facteur important dans l’histoire du succès de la sélection des actions ou des obligations. Ce que je veux dire, c’est que la dérivé Qualité n’a plus d’importance depuis huit ans et demi pour les actions et cinq ans pour la dette souveraine. Ce que je veux dire, c’est que cela pourrait ne pas avoir d’importance pendant encore 80 ans. Ou ça pourrait compter à nouveau dans huit mois. Un système à trois corps est un système chaotique. Comme l’indique l’expression courante, le rendement passé n’est pas une garantie de résultats futurs. En fait, la seule chose que je peux vous promettre, c’est que les performances passées ne vous donneront JAMAIS un algorithme prédictif des résultats futurs dans un système chaotique.

Il s’agit là d’une incertitude de base. C’est la plus grande préoccupation que tout investisseur devrait avoir, que les signaux (dérivés) et les processus (algorithmes) que nous utilisons TOUS pour donner un sens au monde de l’investissement ne sont plus liés aux prix des titres.

… D’accord, Ben, tu m’as épuisé. C’est une façon bizarre et étrange de voir le monde, mais allons-y un instant. Quel est l’intérêt ici ? Que faisons-nous dans un système chaotique ? Qu’est-ce que cela veut dire, dire que nous sommes des investisseurs dans un système chaotique ?

Quatre suggestions.

Premièrement, je pense que nous devrions adopter une philosophie de ce que j’ai appelé l’agnosticisme profond en matière d’investissement, selon laquelle nous ne nous contentons pas de dire que personne n’a de boule de cristal dans ce système, mais que nous sommes plutôt ennuyés par ceux qui insistent pour prétendre en avoir. Je pense que les stratégies d’équilibrage des risques ont beaucoup de sens dans un système chaotique, de sorte que nous pensons d’abord à budgétiser nos risques avec agnosticisme dans toutes les régions géographiques et toutes les catégories d’actifs et secteurs, et ensuite à penser à budgétiser nos dollars.

Deuxièmement, et dans le même ordre d’idées, je pense que nous devrions adopter une stratégie classique de théorie des jeux pour traiter les systèmes incertains – les regrets minimax. L’idée est simple, mais les implications sont profondes : au lieu de chercher à maximiser les rendements, nous cherchons à minimiser notre regret maximum. Gardez à l’esprit que notre plus grand regret n’est peut-être pas une perte ruineuse ! Je connais beaucoup de gens dont le plus grand regret est de ne pas être à la hauteur des Jones. En fait, du point de vue du modèle d’affaires, c’est plus courant qu’improbable. Ou si vous avez acheté du Bitcoin au dessus de 15 000 $ la pièce, je pense que vous savez aussi de quoi je parle. Le fait est que nous devons être douloureusement honnêtes avec nous-mêmes au sujet de nos sources de regret et cibler nos investissements en conséquence. Si nous pouvons être aussi honnêtes avec nous-mêmes, c’est une stratégie TRÈS puissante.

Troisièmement, je pense que nous devrions reconsidérer notre approche à l’égard des stratégies de placement informatisées, c’est-à-dire utiliser les ordinateurs d’une manière anthropomorphique, où nous les traitons comme des humains plus intelligents, plus rapides, lâchés dans un vaste champ de données historiques pour chercher des modèles et des algorithmes… c’est une chasse aux bécassines. Ou du moins, je pense que nous avons extrait à peu près tout le jus de cette orange inductive que nous étions susceptibles d’obtenir. Avec la puissance de traitement massive à portée de main aujourd’hui, sans parler de la puissance de traitement accrue que l’informatique quantique apportera à l’avenir, il y a beaucoup plus à faire avec des approches calculatoires qui adoptent une stratégie plus déductive et tournée vers l’avenir.

Quatrièmement, et c’est peut-être le plus important, je pense que nous devons accepter le fait que nous n’arriverons jamais à comprendre pleinement la réalité d’un système chaotique, mais que cela n’a jamais été aussi important d’essayer. Le cerveau des abeilles et des humains est câblé pour les algorithmes. Les deux espèces voient des tendances même lorsqu’elles n’existent pas, et les deux espèces ont tendance à avoir de mauvais résultats dans des environnements où les signaux dérivés sont en proie à une incertitude de base plutôt qu’à un simple risque de base. Chaque abeille dans le monde suivra ses algorithmes câblés jusqu’à la mort. Et la plupart des humains le feront aussi. Mais les humains ont la capacité de penser au-delà de leur programmation biologique et culturelle… s’ils y travaillent.

Où perdons-nous ces bonnes personnes ? Quand ils se convainquent qu’ils ont trouvé La Réponse – soit sous la forme d’une personne charismatique, soit, plus dangereusement encore, d’une idée charismatique – dans un système chaotique où aucune réponse n’existe, un système chaotique comme les marchés, certes, mais aussi un système chaotique comme la politique.

La réponse est, par nature, totalitaire. Pourquoi ? Parce que c’est une solution générale sous forme fermée. C’est la définition technique de La Réponse, et c’est la définition pratique de la pensée totalitaire. Nous sommes bien décidés à vouloir l’algorithme global, c’est pourquoi il est si difficile d’y résister. Mais si on se soucie de la liberté, si on se soucie de la justice, si nous nous soucions de la liberté et de la justice pour tous… nous devons résister à La Réponse.

Parce qu’on a perdu assez de bonnes personnes.

Aussi sages que des serpents, aussi inoffensifs que des colombes…

W. Ben Hunt
Note du Saker Francophone
Cet article nous intéresse bien plus pour ses aspects de compréhension des systèmes complexes que pour leur application au système financier. Il est le premier d’une série de cinq qui vont s’étaler sur un gros mois.

Traduit par Hervé pour le Saker Francophone

Dimethyltryptamine dmt

Système solaire vortex

Le grand sens – Satprem

(Satprem)

C’est le temps du Grand Sens.

Nous regardons à droite ou à gauche, nous construisons des théories, réformons nos Eglises, inventons des super-machines, et nous descendons dans la rue pour briser la Machine qui nous étouffe, nous nous débattons dans le petit sens. Quand le bateau terrestre est en train de couler, est-ce qu’il importe que les passagers coulent à droite ou à gauche, sous un drapeau noir ou rouge, ou bleu céleste? Nos Eglises ont déjà coulé: elles réforment leur poussière. Nos patries nous écrasent, nos machines nous écrasent, nos Ecoles nous écrasent, et nous construisons davantage de machines pour sortir de la Machine. Nous allons sur la lune, mais nous ne connaissons pas notre propre cœur ni notre destin terrestre. Et nous voulons améliorer l’existant – mais ce n’est plus le temps d’améliorer l’existant : est-ce qu’on améliore la pourriture ? – C’est le temps d’AUTRE CHOSE. Autre chose, ce n’est pas la même chose avec des améliorations.

Mais comment procéder?

On nous prêche la violence, ou la non-violence. Mais ce sont les deux visages d’un même Mensonge, le oui et le non d’une même impuissance : les petits saints ont fait faillite avec le reste, et les autres veulent prendre le pouvoir – quel pouvoir ? Celui des hommes d’Etat ? Est-ce que nous allons nous battre pour détenir les clefs de la prison? Ou pour construire une autre prison? Ou est-ce que nous voulons en sortir vraiment ? le pouvoir ne sort pas de la poudre des fusils, pas plus que la liberté ne sort du ventre des morts – voilà trente millions d’années que nous bâtissons sur des cadavres, des guerres, des révolutions. On prend les mêmes et on recommence. Peut-être est-il temps de bâtir sur autre chose, et de trouver la clef du vrai Pouvoir ?

Voici ce que dit le Grand Sens :
Il dit que nous sommes nés il y a tant de millions d’années – une molécule, un gène, un morceau de plasma frétillant – et nous avons fabriqué un dinosaure, un crabe, un singe. Et si notre œil s’était arrêté en cours de route, nous aurions pu dire avec raison (!) que le Babouin était le sommet de la création, et qu’il n’y a rien de mieux à faire, ou peut-être à améliorer nos capacités de singes et à faire un Royaume Uni des Singes… Et peut-être commettons-nous la même erreur aujourd’hui dans notre forêt de béton. Nous avons inventé des moyens énormes au service de consciences microscopiques, des artifices splendides au service de la médiocrité, et davantage d’artifices pour guérir de l’Artifice… Mais l’homme est-il vraiment le but de tous ces millions d’années d’effort – le baccalauréat pour tous et la machine à laver ?

Le Grand Sens, le Vrai Sens nous dit que l’homme n’est pas la fin. Ce n’est pas le triomphe de l’homme que nous voulons, pas l’amélioration du gnome intelligent – c’est un autre être sur la terre, une autre race parmi nous.

Sri Aurobindo l’a dit : l’homme est un être de transition.
Nous sommes en plein dans cette transition, elle craque de tous les côtés : au Biafra, en Israël, en Chine, sur le Boul’Mich’. L’homme est mal dans sa peau.

Et le Grand Sens, le Vrai Sens nous dit que la seule chose à faire est de nous mettre au travail pour trouver le secret de la transition, le « grand passage » vers l’être nouveau – comme un jour nous avons trouvé le passage du singe à l’homme – et de collaborer à notre propre évolution au lieu de tourner en rond et de prendre les faux pouvoirs pour régner sur une fausse vie.

Mais où est le levier de la Transmutation?

Il est dedans.

Il y a une Conscience dedans, il y a un Pouvoir dedans, celui-là même qui poussait dans le dinosaure, le crabe, le singe, l’homme – qui pousse encore, qui veut plus loin, qui se revêt d’une forme de plus en plus perfectionnée à mesure que son instrument grandit, qui crée sa propre forme. Si nous saisissons le levier de ce Pouvoir-là, c’est lui qui créera sa nouvelle forme, c’est lui le levier de la Transmutation. Au lieu de laisser l’évolution se dérouler à travers des millénaires de tentatives infructueuses, douloureuses, et de morts inutiles et de révolutions truquées qui ne révolutionnent rien, nous pouvons raccourcir le temps, nous pouvons faire de l’évolution concentrée – nous pouvons être les créateurs conscients de l’Etre nouveau.

En vérité, c’est le temps de la Grande Aventure. Le monde est fermé, il n’y a plus d’aventures au-dehors : seuls les robots vont sur la lune et nos frontières sont partout gardées – à Rome ou à Rangoon, les mêmes fonctionnaires de la grande Mécanique nous surveillent, poinçonnent nos cartes, vérifient nos têtes et fouillent nos poches – il n’y a plus d’aventure au-dehors ! L’Aventure est Dedans – la Liberté est dedans, l’Espace est dedans, et la transformation de notre monde par le pouvoir de l’Esprit. Parce que, en vérité, ce Pouvoir était là depuis toujours, suprême, tout-puissant, poussant l’évolution : c’était l’Esprit caché qui grandissait pour devenir l’Esprit manifesté sur la terre, et si nous avons confiance, si nous voulons ce suprême Pouvoir, si nous avons le courage de descendre dans nos coeurs, tout est possible, parce que Dieu est en nous.

SATPREM
Pondichéry,
le 27 juin 1969.

Il faut aller sur le chemin où toutes les soifs s’en vont.
Alors, la femme tire les rêves de l’homme dans la matière,
et l’homme tire la force de la femme dans la lumière,
et ils marchent ensemble.
Si elle ne monte pas, elle le détruit.
S’il ne crée pas, il la perd…

Parce qu’elle est là il peut créer et se développer,
Si elle n’est pas là il ne peut pas créer.
Il y a deux sortes de femmes,
la femme qui est comme une racine, et la femme qui est comme une liane.

(Citation extraite à la volée d’une vidéo dont j’aimerais d’ailleurs retrouver la trace)

Musique des sphères

Il s’agit d’une interprétation sonore des ondes électromagnétiques enregistrées dans l’espace.

« Ainsi, en raison du vide qui entoure la galaxie, les enregistrements sonores de la NASA résultent d’ondes électromagnétiques qui émettent des vibrations à la façon des ondes sonores que nous avons sur notre planète. »

Pour plus de détails, voir ici : sur dailygeekshow.com

La Terre en expansion ?

Agroglyphes

4, pierre angulaire du système solaire

Comme le prétendait un certain Albert Einstein, « le hasard c’est le divin qui se promène incognito ! »
» Considérez l’atome et rappelez-vous sans arrêt « Combien » Tout est Un,
et « Comment » Tout est à la fois 4 et 1. » Les HATHOR

Système solaire : Une mathématique du vertige

[Note de J. Frendelvel : l’article ci-dessous est dans sa majeure partie un extrait de l’ouvrage « L’or des étoiles : Nouveau regard sur le système solaire ». Bien qu’il mette en relief une surprenante dynamique dans le système solaire, ce passage n’en est pas moins, en l’occurence, sorti de son contexte. Dans le livre, des approches préléminaires lui donnent plus de force et de clarté]

Résultat d’une longue recherche astronomique, une vaste architecture mathématique particulièrement élaborée met en évidence une troublante « signature » au sein du système solaire. Cette cathédrale céleste présente de multiples facettes : géométrie, phénomènes inversés, jeux de chiffres, etc.

Partant d’un surprenant jeux arithmétique autour du chiffre 4 qui se révèle être la pierre angulaire numérique du système solaire, cet article expose également comment la Terre, la Lune, Vénus et Mercure sont incroyablement reliés mathématiquement aux figures géométriques simples telles que le cercle, le carré, le triangle et le pentagone, ainsi qu’aux volumes dits « de Platon ».

Le mimétisme de Soleil et Lune

Depuis la nuit des temps, Soleil et Lune ont été les deux grands luminaires de notre planète Terre, rythmant la flore et la faune ainsi que la majeure partie des activités humaines qui se sont soumises aux cycles des jours, semaines, mois et années. Leurs dimensions apparentes quasiment similaires engendrent, de temps à autres, des éclipses solaires spectaculaires lorsque la Lune vient s’aligner précisément avec l’astre du jour. Bien qu’exceptionnels, les phénomènes d’occultations totales marquent souvent les esprits de différentes manières.

De nombreuses personnes ont sans doute réalisé, un jour ou l’autre, l’aspect particulièrement insolite de cet évènement. En effet, tandis que la multitude d’étoiles et les quelques planètes illuminant le ciel nocturne, n’apparaissent guère plus grosses que des points, le Soleil et la Lune crèvent l’écran céleste par leurs tailles conséquentes, mais, surtout, nous interpellent sur la singularité incroyable de la similitude de leur envergure apparente.

Ces deux astres nous apparaissent sous forme d’un disque de 0,25 (ou ¼) degré de rayon.

Dans la réalité, ces deux corps ont des dimensions très différentes puisque le Soleil est 400 fois plus grand que la Lune en diamètre. Mais notre satellite étant 400 fois plus proche, ils nous apparaissent ainsi de grandeurs identiques. Au niveau astronomique, la probabilité d’une telle coïncidence est infime. Pourtant ces deux compagnons des jours et des nuits l’ont réussie en jouant avec le chiffre 4.

Grâce à l’observation des tâches qui apparaissent sur le disque solaire, il a été possible de mesurer la rotation de sa surface visible que l’on appelle la photosphère, laquelle s’est avérée être nettement plus rapide à l’équateur qu’aux pôles. L’estimation exacte de la rotation dans les zones polaires est difficile, par contre la zone équatoriale tourne en 25 jours (25,38 j). Ce chiffre 25, image de l’inverse du 4 (puisque 1/4 = 0,25), est donc dès le départ une référence solaire. Il s’agit ici de période de rotation sidérale, c’est-à-dire par rapport aux étoiles lointaines que l’on peut considérer, à notre échelle humaine, comme un repère fixe. Par contre, un point quelconque de cet équateur solaire mettra 27,3 jours pour faire face une seconde fois à la Terre, ceci du fait que notre planète se déplace sur son orbite. Ce laps de temps est appelé rotation synodique du Soleil et il se trouve être curieusement égal à la période de révolution de la Lune autour de la Terre.

Mais, chose encore plus étonnante, durant les dernières années, des astrophysiciens ont découvert que sous la photosphère, un peu plus en profondeur, la masse solaire interne tournait d’un seul bloc en 27 jours et quelques. Ce double synchronisme de la Lune et du Soleil étant tellement anachronique que les autorités scientifiques concernées sont restées très discrète sur ce fait, se gardant même de communiquer au public une valeur plus précise de cette rotation du Soleil interne.

La Lune est une magicienne

Notre inlassable compagne céleste ne s’est pas contentée d’avoir mimé la taille du Soleil et de s’être synchronisée avec lui, elle est également l’auteur de nombreuses autres prouesses, dont beaucoup sont liées avec sa période de révolution sidérale de 27,32 jours.

Commençons par une petite expérience simple et amusante. Inscrivons, sur notre calculette électronique, la valeur de cette révolution lunaire de la manière la plus précise, soit 27,32166. Ensuite, une simple pression sur la touche inverse affichera le résultat 0,036600… Les trois premiers chiffres significatifs 366 nous donnent directement le nombre de rotations (1) de la Terre en un année normale (non bissextile).[ 1- Dans une année calendaire normale, la Terre effectue 366 rotations, mais du fait de sa révolution autour du Soleil, elle ne connaît que 365 journées ou alternances jour/nuit.]

Calculer l’inverse d’un nombre, en l’occurrence 27,32166 , revient à effectuer la division suivante : 1 / 27,32166 = 0,036600…
Si l’on compare la période de notre journée solaire à celle de la révolution lunaire, c’est exactement la même équation qui est posée, c’est-à-dire : 1j / 27,32166j = 0,036600…

Maintenant si l’on compare, non plus la journée solaire terrestre, mais la période de rotation sidérale de la Terre à celle de la révolution de la Lune, l’équation est légèrement différente puisque la période de rotation de la Terre est un peu inférieure aux 24 heures d’une journée. La rotation terrestre s’effectuant en 23 heures 56 minutes et 4 secondes, cela correspond à 0,99727 jour. L’équation s’écrit alors : 0,99727j / 27,32166j = 0,03650… Cette fois, les trois premiers chiffres significatifs nous donnent le nombre de jours dans une année normale de notre calendrier. Voilà déjà une entrée en matière prometteuse.

La Lune et la Quadrature du cercle

Après ce petit jeu arithmétique, abordons quelques aspects plus géométriques. Durant des siècles, de nombreux mathématiciens et experts ont tenté de résoudre l’énigme de la quadrature du cercle, mais sans succès. Le problème consistait, à partir d’un cercle quelconque, à tracer un carré ayant même surface avec comme seuls outils une règle et un compas (figure 5.4).

Fig. 5.4

Le carré ABCD et le cercle de rayon OE ont même surface

Il s’est avéré que cette tentative de dessin géométrique était un casse-tête insoluble sur lequel des générations de chercheurs se sont brisés les dents. Mais pendant tout ce temps, la Lune, un tant soit peu ironique, jouait subtilement avec des variantes de cette quadrature du cercle.

La première de ces variantes est imagée par le graphique 5.5. Le carré et le cercle représentés n’ont pas la même surface comme sur la figure précédente, mais ont, par contre, le même périmètre. Bien que les deux schémas soient ressemblants, les dimensions respectives des deux formes géométriques sont différentes ; sur le second schéma (5.5) on peut constater que les quatre sommets du carré dépassent nettement moins du cercle.

Fig. 5.5

Périmètre d’un carré de 1 m de coté = Périmètre d’un cercle d’un diamètre de 1,2732 m

La condition de cette égalité des périmètres est que le diamètre du cercle soit supérieur au côté du carré de 27,32% soit l’image de la révolution sidérale de la Lune. Concrètement, si l’on donne la valeur 1 mètre au côté AB du carré, il faut alors donner la valeur 1 m + 27,32%, soit 1,2732 m, au diamètre EF du cercle.

La seconde variante est abordée avec le schéma 5.6. Il y est tracé une figure extrêmement simple que, sans doute, beaucoup ont réalisé un jour, au moins durant un cours de géométrie, puisqu’il s’agit d’un cercle de rayon OE, inscrit dans un carré ABCD.

Fig. 5.6

Surface du carré = Surface du cercle inscrit + 27,32%
(valeur de la révolution sidérale lunaire)

Dans ce second cas de figure, il s’avère que la surface du carré est supérieure de 27,32% à la surface du cercle inscrit, soit de nouveau la valeur (27,32 jours) de la révolution lunaire.
Le cercle est la représentation bi-dimensionnelle des sphères célestes, tandis que le carré est la forme géométrique par excellence liée au chiffre 4 en ayant 4 côtés égaux et 4 angles égaux. Ainsi la Lune, relie ces deux figures en nous apportant à sa manière une solution de la quadrature du cercle.
Mercure et triangle

Par ailleurs, ce jeu de figures géométriques peut être prolongé de la sorte. Sur le schéma 5.7 nous trouvons un triangle équilatéral EFG inscrit dans le cercle de rayon OE. Une comparaison des surfaces du cercle et du triangle nous montre alors qu’on peut obtenir l’aire du triangle en diminuant celle du cercle de 58,65%.
Cette fois, c’est la valeur de la rotation sidérale de la planète Mercure (58,65 jours) que l’on retrouve dans ce rapport entre un cercle et son triangle équilatéral inscrit.

Fig. 5.7

Surface du triangle inscrit = Surface du cercle – 58,65%
(valeur de la rotation sidérale de Mercure)

Vénus et pentagone

Continuons sur notre lancée avec le graphique 5.8 qui représente un pentagone régulier JKLMN inscrit dans un cercle. En leur appliquant la même démarche de comparaison des surfaces respectives il faudra cette fois diminuer l’aire du cercle de 24,3% pour obtenir celle du pentagone.
En l’occurrence, il s’agit maintenant de l’image de la valeur de la rotation sidérale de Vénus, laquelle est de 243 jours.

Fig. 5.8

Surface du pentagone inscrit = Surface du cercle – 24,3%
(image de la valeur de la rotation sidérale de Vénus : 243 jours)

Nous avons donc affaire à 4 figures de base de la géométrie à savoir : le cercle, le triangle, le carré et le pentagone. Il s’avère ainsi que les 4 premiers astres compagnons du Soleil : Mercure, Vénus et le couple Terre-Lune, sont venus marquer de leur empreinte les rapports de surface des 4 figures géométriques de base que sont le cercle et les 3 premiers polygones réguliers.

Sphère et cube

Après l’étude que nous venons de faire sur les formes géométriques planes de base, évoluons maintenant vers les volumes. Sur le dessin 5.9 on peut voir une boule C intégrée à l’intérieur d’un cube B, lui-même à l’intérieur d’une sphère A. Il va de soit que B est le plus grand cube que la sphère A puisse contenir, ses 8 sommets touchant la surface interne de la sphère. Il en va de même pour la petite boule C dont la surface est en contact avec les 6 parois du cube B qui la contient.

Fig. 5.9 Sphères et cube imbriqués

Puisque nous voilà en présence d’objets en trois dimensions, l’intérêt est maintenant de comparer les volumes réciproques de ces formes très spécifiques afin de voir si on y trouve également des coïncidences particulières avec les planètes du système solaire.

Il s’avère en fait que la grande sphère A contient 2,721 fois plus que le cube B qui lui est intérieur. Bien que l’image de cette valeur se rapproche étonnamment de celle de la révolution sidérale de la Lune qui est de 27,32 jours, toutefois elle en diffère un peu. Un rapide coup d’œil sur les caractéristiques lunaires, nous permet de constater qu’en fait ce rapport du volume de la sphère au volume du cube qu’elle contient, est précisément l’image de la valeur de la révolution draconitique(2) de la Lune qui vaut 27,21 jours ! [ 2-La révolution draconitique lunairee est le laps de temps entre deux passages successifs de la Lune à son noeud ascendant. Elle s’avère légèrement différente de la révolution sidérale du fait du fait d’une perturbation cyclique de l’orbite lunaire et constitue un cycle très important qui permet d’étudier et de prévoir les éclipses. En effet, la période séparant deux éclipses est obligatoirement un multiple exact de la révolution draconitique lunaire de 27,21 jours.]

De son côté le volume de la petite sphère interne C équivaut à 0,524 fois le volume du cube B. C’est un nombre que l’on retrouve également dans la partie décimale de la distance moyenne au Soleil de la planète Mars, laquelle vaut 1,524 UA. On le retrouve encore dans le déplacement journalier de cette même planète autour du Soleil ; Mars effectuant sa révolution de 360° autour du Soleil en 687 jours, sa progression moyenne par jour sur son orbite est de 360° / 687 j = 0,524 degré. Sous sa forme arrondie ce nombre 0,524 est une image du 52 que nous allons découvrir plus avant.

Il nous reste une dernière comparaison à explorer dans le schéma 5.9, c’est le rapport des volumes de deux formes géométriques identiques consécutives. Dans le cas de la figure 5.9, il s’agit des deux sphères A et C. Il se trouve qu’en passant de la petite sphère à la grande sphère, le volume est multiplié par 5,2. De nouveau, émerge ce nombre miroir de 2,5, somme de 2,5 et 2,7, que nous avons maintes fois rencontré [cf livre] et qui représente aussi la distance solaire moyenne de Jupiter (5,2 unités astronomiques). Pour être tout à fait précis, ce rapport de deux sphères consécutives (ou deux cubes consécutifs) est de 5,196 soit 5,2 moins 0,004. Sa valeur exacte s’écrit plus concrètement : , puisque 5,196 * 5,196 = 27.

Finalement, l’étude des volumes des sphères et cubes imbriqués les uns dans les autres met en évidence les mêmes nombres clés que nous avons découvert dans la dynamique du système solaire [cf livre]. De plus, notre satellite naturel se montre intimement lié aux relations entre le cercle et le carré par la valeur de sa révolution sidérale de 27,32 jours, ainsi qu’entre la sphère et le cube par la valeur de sa révolution draconitique de 27,21 jours. Décidément la Lune recèle bien des secrets.

Mercure et tétraèdre

En dernier lieu, voici maintenant (figure 5.10) une sphère contenant un tétraèdre régulier, lequel, avec le cube, est l’un des cinq volumes dits de Platon(3).[ 3 Les cinq volumes réguliers dits de Platon sont le tétraèdre (4 faces triangulaires), le cube (6 faces carrées), l’octaèdre (8 faces triangulaires), le dodécaèdre (12 faces pentagonales) et l’icosaèdre (20 faces triangulaires).]

Fig. 5.10

Tétraèdre à l’intérieur d’une sphère.

Volume du tétraèdre = Volume de la sphère – 88% .

Un tétraèdre est une pyramide à base triangulaire, il fait à la fois référence au 4 par ses 4 faces et au 3 par ses côtés triangulaires. Son volume s’obtient en diminuant le volume de la sphère de 88%.
C’est maintenant qu’il devient intéressant de mettre face à face ce rapport sphère/tétraèdre avec le rapport cercle/triangle (figure 5.7) qui a été étudié un peu auparavant.

Premier rappel :

Surface du triangle inscrit = surface du cercle – 58,65%
Second rappel :
Volume du tétraèdre contenu = volume de la sphère – 88%

Le premier pourcentage de 58,65%, nous l’avions déjà vu, est l’image de la rotation sidérale de Mercure (58,65 jours), tandis que le second de 88% se trouve être l’image de la période de révolution de Mercure autour du Soleil (88 jours). Ainsi les paramètres de Mercure se trouvent étroitement imbriqués dans les rapports du cercle au triangle et de la sphère au tétraèdre. Le triangle avec ses 3 angles et ses 3 côtés ainsi que le tétraèdre avec ses faces triangulaires font de la sorte référence au nombre 3, tout comme Mercure dont la longue journée solaire de 176 jours terrestres dure le temps de 3 de ses rotations (3 fois 58,65 jours).

La Terre jongle avec le 4

Mais revenons vers la Terre car elle aussi semble très douée pour jouer habilement avec le chiffre 4. Le calendrier qu’on utilise se veut être le fidèle reflet des 4 saisons. Cela signifie qu’il se base non pas sur l’année sidérale, mais sur une période très légèrement différente qui est le laps de temps précis entre deux équinoxes de printemps(4). [ 4 Ces deux périodes sont légèrement différentes du fait d’une instabilité de l’axe des pôles qu’on appelle précession des équinoxes. Cet axe polaire est en effet animé d’un lent mouvement décrivant un cone selon un cycle d’environ 26000 ans.] Cette année tropique, comme on la nomme, est de 365,242 jours, soit très proche de 365 ¼ jours. En conséquence, puisque le nombre de journées dans une année n’est pas un nombre entier exact, le calendrier julien, instauré par l’empereur romain Jules César, a introduit tous les 4 ans une année bissextile. Ce qui signifie que les années dont le millésime est divisible par 4, comportent un jour de plus afin que l’équinoxe de printemps (dans l’hémisphère nord) reste calé sur la date du 21 mars. Au 16ème siècle, on s’est aperçu que cette manière de faire n’était pas encore assez précise puisque un décalage de 10 jours s’était formé au cours des siècles. En 1582, le pape Grégoire XIII institua alors le calendrier grégorien, celui en vigueur de nos jours. Outre le rattrapage immédiat de 10 jours(5), ce nouveau calendrier supprimait de plus les années bissextiles lors des années séculaires (celles qui se terminent par deux zéro) comme 1700, 1800, 1900, etc.[ 5 En France la réforme du calendrier a été appliquée en décembre 1582. Ainsi, le lendemain du dimanche 9 décembre 1582 fût le lundi 20 décembre 1582.] Toutefois les années séculaires divisibles par 400 comme 1600 et 2000 restaient bissextiles, tout ceci afin d’adapter au mieux le calendrier à la réalité astronomique. Pour résumé, tous les 4 ans, l’année est bissextile, exceptées les années séculaires, mais tous les 4 siècles, on en remet une ; voilà encore un magnifique jeu de 4.

Comme nous l’avons vu, en une année normale, la Terre effectue 366 rotations sur elle-même, mais, puisqu’elle effectue un mouvement de révolution autour du Soleil dans le même laps de temps, nous ne connaissons que 365 alternances jour/nuit. De ce fait, ces deux périodes, rotation sidérale et journée(6), n’ont pas tout à fait la même valeur.[ 6 La journée terrestre de 24 heures est une rotation synodique de la Terre par rapport au Soleil.] La journée fait 24 heures par définition tandis que la rotation sidérale est de 23 heures 56 minutes et 4 secondes. Cette dernière est donc inférieure d’environ 4 minutes ou, plus précisément, de 4 minutes moins 4 secondes.

Traduit d’une autre manière, la durée d’une rotation de la Terre est inférieure de 27,32°/ooo (pour dix mille) à la journée terrestre ; encore un curieux reflet des 27,32 j de la période de révolution lunaire.

Le chiffre 4 se retrouve encore dans la valeur de la circonférence de la Terre qui est, rappelons-le, de 40000 kilomètres (un 4 suivi de 4 zéros). Ceci étant d’ailleurs une conséquence de la manière dont, par le passé, l’étalon mètre a été instauré. Mesure qui, à l’origine, a été définie comme étant la dix millionième partie du quart du méridien terrestre. De ceci il ressort qu’une personne, demeurant à l’équateur terrestre, parcourt, avec le mouvement giratoire de la Terre et à quelques kilomètres près, une distance de 40000 km en 24 heures. Dans le même laps de temps de 24 heures terrestres, le Sélénien(7) de service posté sur l’équateur de la Lune, aura parcouru, avec la rotation de son astre, précisément 100 fois moins de distance respective, soit 400 kilomètres.[ 7 Un Sélénien est un habitant supposé de la Lune.] Nous savons déjà que le Soleil, tout en étant 400 fois plus distant que la Lune, à une taille 400 fois supérieure à celle-ci. De même, un « habitant fictif » de l’équateur solaire est entraîné dans un mouvement de giration de 400² (160000) kilomètres par jour terrestre soit 4 fois plus vite qu’ici sur Terre. D’autre part, la densité du Soleil se met également de la partie puisque les astrophysiciens l’ont estimée à 1,41 (c’est-à-dire 1,41 fois la densité de l’eau), ce qui est la valeur de , mais peut s’écrire aussi (se lit : quatrième racine de quatre).

Voilà donc des prédispositions aux chiffres et à la géométrie particulièrement étonnantes de la part des astres, mais ceux-ci n’ont pas encore fini de nous étonner dans ce domaine…

http://frendelvel.free.fr/

Loin des théories chaotiques avancées en guise d’explication par les astronomes,
une surprenante architecture géométrique et arithmétique est à l’oeuvre.

Devant les progrès de la science, l’idée d’une intelligence organisatrice sous-jacente, d’un quelconque Grand Architecte qui aurait apposé de la sorte sa signature, est-elle encore envisageable aujourd’hui ? Et dans ce cas, comment la déceler ? L’une des voies possibles est l’étude mathématique de deux structures en forme de disque fort dissemblables : les anneaux de Saturne et la ceinture principale d’astéroïdes (…).